Hôm nay, 05/09/2016, tôi bắt đầu dạy môn Giải tích điều hòa cho K58TN.
Đề cương môn học các bạn xem
3_Phu luc 2-Mau de cuong hoc phan_GiaiTichDieuHoa
Tôi sẽ sử dụng cuốn
“An introduction to Harmonic Analysis”, Y. Katznelson,
như tài liệu chính.
Hôm nay, 05/09/2016, tôi bắt đầu dạy môn Giải tích điều hòa cho K58TN.
Đề cương môn học các bạn xem
3_Phu luc 2-Mau de cuong hoc phan_GiaiTichDieuHoa
Tôi sẽ sử dụng cuốn
“An introduction to Harmonic Analysis”, Y. Katznelson,
như tài liệu chính.
Về độ đo Borel và độ đo Borel phức, Định lý Fubini-Tonelli, Định lý đổi biến các bạn tham khảo cuốn
“Real Analysis: Modern techniques and their applications”, G. Folland,
hay
“Real and Complex Analysis”, W. Rudin.
Về giải tích điều hòa trừu tượng, liên quan đến nhóm tô-pô, độ đo Haar, các bạn tham khảo cuốn
“A course in abstract Harmonic Analysis”, G. Folland,
hay
“Fourier Analysis on Groups”,W. Rudin.
Các bạn có thể tìm cuốn của Katznelson theo đường link
Click to access Katznelson%20Y.%20An%20Introduction%20To%20Harmonic%20Analysis%20(CUP,%202004)(299s)_MCf_.pdf
Tính bất biến chuẩn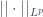 của phép dịch chuyển chính là tích phân của hàm tuần hoàn trên mỗi chu kỳ như nhau. Có được tính bất biến này nhờ:
của phép dịch chuyển chính là tích phân của hàm tuần hoàn trên mỗi chu kỳ như nhau. Có được tính bất biến này nhờ:
+ tính tuần hoàn của hàm,
+ tính bất biến với phép dịch chuyển của độ đo Lebesgue (đặc trưng của độ đo Haar).
Ta quan sát điều này qua hình ảnh:
Có
Do độ đo Lebesgue bất biến với phép dịch chuyển nên
Do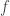 tuần hoàn nên
tuần hoàn nên
Lại tiếp tục dùng tính bất biến của độ đo ta sẽ dẫn đến điều phải chứng minh.
Hôm nay 12/09/2016 tôi có nhờ một số bạn lên làm bài tập. Có thể thấy công việc lại là tính tích phân xác định.
Ngoài ra trong khi nói tiếp về lý thuyết có một vài bài tập sau:
1. Cho là không gian Banach trên trường phức,
là không gian Banach trên trường phức, ![\varphi:[0, 2\pi]\to B](https://s0.wp.com/latex.php?latex=%5Cvarphi%3A%5B0%2C+2%5Cpi%5D%5Cto+B&bg=ffffff&fg=333A42&s=0&c=20201002) là hàm liên tục. Chứng minh rằng dãy
là hàm liên tục. Chứng minh rằng dãy
là dãy Cauchy trong
2. Cho là không gian Banach thuần nhất,
là không gian Banach thuần nhất, 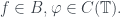 Chứng minh ánh xạ
Chứng minh ánh xạ
là ánh xạ liên tục từ vào
vào 
Trong trường hợp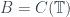 hãy chứng minh dãy hàm
hãy chứng minh dãy hàm
hội tụ đều đến tích phân Riemann
trên
3. Cho dãy số thực hội tụ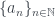 . Chứng minh dãy trung bình sau
. Chứng minh dãy trung bình sau
cũng hội tụ. Hơn nữa hai dãy này có cùng giới hạn.
Ngoài ra các bạn nên làm các bài tập cuối mỗi mục trong sách của Katznelson.
Về thuật ngữ “nhân khả tổng” Katznelson dùng “summability kernels”. Trong
“Fourier Analysis: an introduction”, E. M. Stein, R. Shakharchi,
lại dùng “good kernels”,
còn trong
“Introduction to Fourier Analysis and Wavelets”, M. A. Pinsky,
lại dùng “approximate identity”.
Trên lớp tôi có đưa ví dụ:
+ nhân Dirichlet không khả tổng,
không khả tổng,
+ nhân Fejer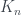 khả tổng.
khả tổng.
Ngoài nhân Poisson
cũng khả tổng.
Một số nhân khả tổng khác xây dựng từ nhân Fejer:
+ nhân Valle de Poussin ,
,
+ nhân Jackson .
.
Ngoài ra trong bài giảng tôi còn nói: đồng cấu nhóm liên tục
là biểu diễn 1-chiều phức của nhóm cộng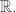
Chú ý với nhóm hữu hạn ta gắn tô-pô rời rạc thì đồng cấu nhóm đương nhiên liên tục. Nhóm không hữu hạn như nhóm các số nguyên cũng vậy.
cũng vậy.
Về xấp xỉ đồng nhất, approximate identity, các bạn tham khảo thêm
Xấp xỉ đồng nhất
Cho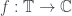 xác định như bài 1/ tr. 6, sách Katznelson,
xác định như bài 1/ tr. 6, sách Katznelson,
Ký hiệu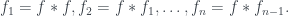 Có thể thấy rằng
Có thể thấy rằng
Khi đó ta có hình ảnh của việc lấy tích chập:
Từ hình vẽ ta có cảm giác:
Các bạn thử giải thích xem sao?
Bài tập theo chủ đề:
– bạn P. M. Hoàng chọn: bài về việc đánh giá tốc độ hội tụ theo chuẩn, cụ thể các bài 1, 2, 5 trong section 3, chapter 1 trong sách của Katznelson;
– bạn T. M. Tâm chọn: phổ của toán tử unitary, liên quan đến section 7, chapter 1 trong sách Katznelson;
– bạn N. T. Trung chọn: định lý biểu diễn Riesz, đọc trong Rudin hoặc Folland;
– bạn L. Q. Tuấn chọn: bài về hàm đặc trưng, cụ thể các bài 7-16 trong section 1, chapter 1trong sách Katznelson.
Đồ thị nhân Dirichlet
– khi
– khi
– khi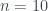
Đồ thị nhân Fejer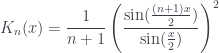
– khi
– khi
-khi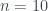
So sánh sự thay đổi của nhân Dirichlet và nhân Fejer
Hiện tượng Gibb liên quan đến hàm
Hiện tượng Gibb của hàm lẻ, tuần hoàn chu kỳ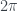 , cho bởi
, cho bởi
nhìn qua hình
Một trong những điểm chú ý của hiện tượng Gibb nhìn được từ hình vẽ:
– bước nhảy của hàm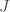 tại 0 bằng 1,
tại 0 bằng 1,
– bước nhảy của chuỗi Fourier tại 0 là gần bằng 1.179.
gần bằng 1.179.
Vẽ hình này nhờ Maple như sau:
Hàm
có đồ thị
là hàm khả vi liên tục, với đạo hàm của nó có đồ thị
Chú ý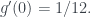
Một bạn có hỏi: hàm liên tục thì có biến phân bị chặn không?
Phản ví dụ như sau:
Hàm này liên tục nhưng dao động mạnh tại gốc:
Đây cũng là so sánh dấu hiệu Dini và dấu hiệu Jordan về hội tụ điểm của tổng Dirichlet. Chi tiết các bạn xem trong tiểu luận của T.Q.Phong, trang 29-30:
Tiểu luận TQPhong
Ta có phép nhúng
trong đó![AC([0, \pi])](https://s0.wp.com/latex.php?latex=AC%28%5B0%2C+%5Cpi%5D%29&bg=ffffff&fg=333A42&s=0&c=20201002) là không gian các hàm liên tục tuyệt đối,
là không gian các hàm liên tục tuyệt đối, ![Lip([0, \pi])](https://s0.wp.com/latex.php?latex=Lip%28%5B0%2C+%5Cpi%5D%29&bg=ffffff&fg=333A42&s=0&c=20201002) không gian các hàm Lipschitz.
không gian các hàm Lipschitz.
Chú ý rằng không gian các hàm Holder![C^\alpha([0, \pi]), 0< \alpha < 1,](https://s0.wp.com/latex.php?latex=C%5E%5Calpha%28%5B0%2C+%5Cpi%5D%29%2C+0%3C++%5Calpha+%3C+1%2C&bg=ffffff&fg=333A42&s=0&c=20201002) không nằm trong
không nằm trong ![BV([0, \pi])](https://s0.wp.com/latex.php?latex=BV%28%5B0%2C+%5Cpi%5D%29&bg=ffffff&fg=333A42&s=0&c=20201002) . Tuy nhiên theo dấu hiệu Dini chuỗi Fourier của hàm Holder hội tụ về đúng hàm đó.
. Tuy nhiên theo dấu hiệu Dini chuỗi Fourier của hàm Holder hội tụ về đúng hàm đó.
Cũng cần chú ý thêm: hàm khả vi chưa chắc có biến phân bị chặn, chẳng hạn hàm![f:[-\pi, \pi]\to\mathbb R](https://s0.wp.com/latex.php?latex=f%3A%5B-%5Cpi%2C+%5Cpi%5D%5Cto%5Cmathbb+R&bg=ffffff&fg=333A42&s=0&c=20201002)
Tôi nhầm: Ta không có phép nhúng
Chẳng hạn hàm liên tục tuyệt đối và không Lipschitz.
liên tục tuyệt đối và không Lipschitz.
Ta có
Khi bạn Trung trình bày về các định lý Riesz, tôi có hỏi về tính Hausdorff. Các bạn có thể tham khảo thêm về các tiên đề tách (separation axiom)
https://en.wikipedia.org/wiki/Separation_axiom
Bổ đề Urysohn liên quan trực tiếp đến tính chuẩn tắc của không gian tô-pô:
https://en.wikipedia.org/wiki/Urysohn%27s_lemma
Chú ý không gian Hausdorff compact địa phương có thể không chuẩn tắc. Chẳng hạn
http://math.stackexchange.com/questions/235729/locally-compact-hausdorff-space-that-is-not-normal
Về biến phân toàn phần của độ đo phức các bạn tham khảo
Click to access complex.pdf
hay
https://en.wikipedia.org/wiki/Complex_measure
Về phổ liên tục, phổ rời rạc của toán tử unitary sinh bởi phép biến đổi bảo toàn độ đo các bạn tham khảo trang 48 và 68 trong cuốn
“An Introduction to Ergodic Theory”, Peter Walters.
Hôm nay tôi chuyển sang phần tích phân Fourier trên đường thẳng. Một trong các điểm khác cơ bản so với chuỗi Fourier: đường thẳng không compact. Điều này dẫn đến việc định nghĩa biến đổi Fourier trong gặp đôi chút khó khăn. Tôi trình bày ba cách tiếp cận:
gặp đôi chút khó khăn. Tôi trình bày ba cách tiếp cận:
C1: sử dụng việc xấp xỉ bởi hàm giảm nhanh;
C2: sử dụng việc xấp xỉ bởi các hàm đơn giản;
C3: sử dụng hàm Hermite.
Về cơ bản tính chất của biến đổi Fourier và chuỗi Fourier có nhiều điểm tương đồng. Trong một vài chứng minh tôi có sử dụng kết quả của chuỗi Fourier để chứng minh cho biến đổi Fourier.
Bài tập tiếp:
– bạn Trung: tìm hiểu độ đo Haar,
– bạn Tâm: tìm hiểu về Định lý Bochner về biến đổi Fourier của độ đo Borel,
– bạn Tuấn: tìm hiểu hàm đặc trưng trên trường p-adic.
Tuần tới, hai bạn Tuấn, Hoàng chuẩn bị trình bày.
Tôi xem bài nộp của Trung, Tâm thấy: các bạn chưa chi tiết thêm ý hiểu của mình, đôi khi còn bỏ những chi tiết quan trọng. Tuần sau tôi sẽ trả lại và hy vọng các bạn sửa lại bài viết cho hợp lý hơn.
Khi chứng minh bất đẳng thức, khá gần bất đẳng thức Heisenberg, tôi có sử dụng:
nếu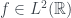 có
có 
thì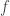 liên tục tuyệt đối, khả vi hầu khắp nơi và
liên tục tuyệt đối, khả vi hầu khắp nơi và  có
có
Tuy nhiên, chú ý và không biết có hay không
và không biết có hay không
Khi đó tôi mắc phải:
tại sao ?
?
Một điểm khác trong bài giảng liên quan đến “tổng Riemann”
hội tụ đến tích phân
khi .
.
Các bạn thử giải thích chi tiết khi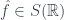 .
.
Hôm nay hai bạn Tuấn và Hoàng đã trình bày bài tập lần 1.
Bài tập lần 2:
– Bạn Trung: tìm hiểu việc xây dựng độ đo Haar trên nhóm compact địa phương, đặc biệt là các nhóm cụ thể nhóm nhân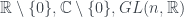 và nhóm
và nhóm 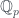 . Bạn tham khảo mục 2.2 trong cuốn “A course in abstract harmonic analysis” của G. Folland.
. Bạn tham khảo mục 2.2 trong cuốn “A course in abstract harmonic analysis” của G. Folland.
– Bạn Tâm: tìm hiểu về biến đổi Fourier của độ đo Borel. Bạn tham khảo mục VI. 2 trong sách “An introduction to harmonic analysis” của Y. Katznelson.
– Bạn Tuấn: tìm hiểu về hàm đặc trưng của nhóm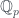 .Bạn tham khảo mục 4.1 trong cuốn “A course in abstract harmonic analysis” của G. Folland.
.Bạn tham khảo mục 4.1 trong cuốn “A course in abstract harmonic analysis” của G. Folland.
– Bạn Hoàng: tìm hiểu về xấp xỉ bởi đa thức lượng giác. Bạn tham khảo mục I.8 trong sách “An introduction to harmonic analysis” của Y. Katznelson.
Bài tập lần 1 của bạn Tuấn:
– Bài 11 về dạng mũ của đồng cấu nhóm liên tục: đã làm chưa đúng trên lớp nhưng sửa lại vẫn không đúng. Ý đầu của bài là tập ảnh nằm trên đường tròn bạn làm đúng. Ý sau ngoài dạng còn có các dạng
còn có các dạng
Để có điều này ta xét nhóm con hạt nhân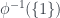 .
.
– Bài 13, 15 chưa làm. Bài 13 sử dụng Định lý Steinhauss. Bạn tham khảo
Steinhauss
Bài 15 xét tập
Nếu hoặc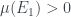 hoặc
hoặc 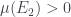 dẫn đến điều vô lý vì khi đó
dẫn đến điều vô lý vì khi đó
có số tự nhiên N để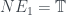 hoặc
hoặc 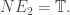
Bài 11 cần thêm bước chứng minh có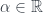 để
để
Bạn Trung chứng minh điều này bằng việc lấy mà
mà 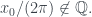 Chú ý
Chú ý 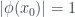 nên có
nên có 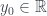 để
để
Lấy Từ tính bảo toàn cấu trúc nhóm có
Từ tính bảo toàn cấu trúc nhóm có
Tiếp tục dùng tính liên tục của và tính trù mật của tập
và tính trù mật của tập 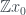 trong
trong  ta có điều phải chứng minh.
ta có điều phải chứng minh.
Trong phần bài tập bạn L. Q. Tuấn còn trình bày lời giải cho bài 16 như sau:
Đồng cấu nhóm đo được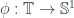 là hàm thuộc
là hàm thuộc  nên có hệ số Fourier
nên có hệ số Fourier
Với mỗi cố định, đổi biến
cố định, đổi biến  có
có
Tích phân cả hai vế theo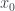 có
có
nên hoặc
hoặc 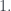
Nếu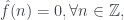 thì
thì 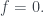 Vô lý.
Vô lý.
Nếu có để
để 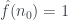 thì từ (1) có
thì từ (1) có
Từ đây ta có ngay lời giải cho bài 11.
Cách này có vấn đề vì có thể lấy hoặc hoặc
hoặc 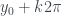 . Khi đó
. Khi đó  sẽ như nào?
sẽ như nào?
Quay trở lại việc xét nhóm hạt nhân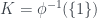 .
.
TH1. Nếu nhóm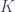 có vô số phần tử thì nó trù mật trong
có vô số phần tử thì nó trù mật trong  nên từ tính liên tục ta có
nên từ tính liên tục ta có 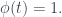
TH2. Nếu nhóm này có hữu hạn phần tử thì nó là nhóm cyclic, nghĩa là có số tự nhiên sao cho
sao cho
Khi đó và
và  Đây chính là điểm để xem
Đây chính là điểm để xem
Nếu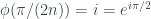 mà
mà 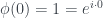
nên dùng tính chất liên tục và bảo toàn cấu trúc nhóm ta có
Từ đó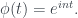
TH còn lại , làm tương tự ta có
, làm tương tự ta có
Để ý rằng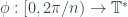 là đơn ánh nên cũng là song ánh.
là đơn ánh nên cũng là song ánh.
Bài tập về đánh giá xấp xỉ tổng Fejer của bạn Hoàng nên làm rõ
+)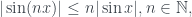
+)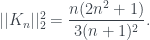
Hôm nay khi trình bày công thức tổng Poisson tôi có nói về hàm zeta và sơ qua về việc dùng công thức Poisson dẫn đến phương trình hàm của hàm zeta. Tiếp đó nói về tập không điểm của hàm zeta không giao với đường . Đây là điểm chốt trong chứng minh của Hadamard và de la Valee-Poussin cho định lý số nguyên tố (Prime Number Theorem). Nếu có thời gian tôi trình bày cách dùng kết quả trên về không điểm hàm zeta và lý thuyết Tauberian để chứng minh định lý số nguyên tố này. Lý thuyết Tauberian dẫn đến niềm tin của Hardy về chứng minh đơn giản cho định lý số nguyên tố. Năm 1948, Selberg và Erdos đã đưa ra chứng minh đơn giản mà không dùng đến hàm zeta. Các bạn tham khảo
. Đây là điểm chốt trong chứng minh của Hadamard và de la Valee-Poussin cho định lý số nguyên tố (Prime Number Theorem). Nếu có thời gian tôi trình bày cách dùng kết quả trên về không điểm hàm zeta và lý thuyết Tauberian để chứng minh định lý số nguyên tố này. Lý thuyết Tauberian dẫn đến niềm tin của Hardy về chứng minh đơn giản cho định lý số nguyên tố. Năm 1948, Selberg và Erdos đã đưa ra chứng minh đơn giản mà không dùng đến hàm zeta. Các bạn tham khảo
https://en.wikipedia.org/wiki/Prime_number_theorem
PNT_ES1
ES_dispute
Bạn Trung trình bày về độ đo Haar trên nhóm compact địa phương còn mắc:
– định nghĩa chính xác nhóm compact địa phương,
– quá trình xây dựng đô đo Haar, cụ thể phiếm hàm tuyến tính dương.
Ngoài ra độ đo Haar cho trường p-adic được trình bày cuối mục 2.2, trang 47 sách Folland.
Bạn Tâm trình bày về định lý Bochner cho độ đo xác suất trên đường thẳng thực còn hạn chế việc tính toán cụ thể trên ví dụ cụ thể.
Bạn Hoàng trình bày về định lý Jackson. Chiều ngược lại cần sử dụng đến bất đẳng thức Bernstein và kỹ thuật tách tổng.
Chú ý: trong phần câu hỏi thi cuối kỳ các bạn chuẩn bị thêm việc chứng minh bất đẳng thức Bernstein:
với là đa thức lượng giác bậc n.
là đa thức lượng giác bậc n.
Trong phần trình bày của bạn Tuấn có nói đến phần lẻ . Khi
. Khi  nó có biểu diễn
nó có biểu diễn
với thỏa mãn
thỏa mãn
Do nên có số nguyên
nên có số nguyên  sao cho
sao cho
Khi đó có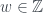 sao cho
sao cho
Do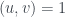 nên
nên 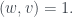
Lại phân tích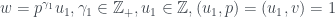 . Khi đó
. Khi đó
Lại làm như trên cho cặp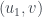 . Cứ thế ta sẽ phân tích được
. Cứ thế ta sẽ phân tích được
với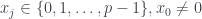 .
.
Khi đó phần lẻ
Từ đây ta định nghĩa hàm
Đây là điểm bạn Tuấn dừng lại ở buổi trình bày sáng này. Tập các hàm đặc trưng, đồng cấu nhóm liên tục
chỉ gồm các hàm dạng
Bài viết của bạn Tâm khá tốt, đặc biệt trình bày hai cách để chỉ ra độ đo Borel dương, hữu hạn có biến đổi Fourier là hàm liên tục, xác định dương:
– chuyển qua TH tuần hoàn (theo Katznelson),
– dùng biến đổi Gelfand (gần giống Folland).
Bạn Tuấn vẫn chưa đến hàm đặc trưng.
Bạn Trung chưa hiểu không gian là không gian tô-pô tích
là không gian tô-pô tích
Khi đó từ tính bảo toàn thứ tự của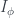 ta có
ta có
Thêm nữa việc xác định độ đo Haar trong một số TH được dẫn từ MĐ 2. 21, chứ không phải kiểm tra chúng thỏa mãn tính bất biến.
Bạn Hoàng viết khá tốt với phần thuận không “đơn giản” như đã trình bày trên lớp mà dùng đến bất đẳng thức Bohr, hay còn gọi là bất đẳng thức ngược Bernstein.
Hôm nay tôi đã kết thúc môn Giải tích điều hòa:
– tóm tắt lại quá trình chứng minh định lý số nguyên tố (Prime Number Theorem)
+ chuyển qua hàm Chebyshev, rồi chuyển từ việc chứng minh định lý sang chứng minh kết quả của Ingham,
+ chuyển từ việc chứng minh kết quả của Ingham qua việc chứng minh định lý Tauberian của Wiener thông qua việc sử dụng hàm zeta Riemann,
+ chứng minh định lý Tauberian của Wiener nhờ lý thuyết về đại số Banach.
Ngoài ra tôi trình bày về sơ lược về đại số Banach và một vài ứng dụng:
+ định lý Wiener về đại số , sau đó dẫn đến định lý Tauberian của Wiener,
, sau đó dẫn đến định lý Tauberian của Wiener,
+ định lý về đại số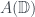 , sau đó đề cập đến định lý corona cho đại số
, sau đó đề cập đến định lý corona cho đại số 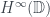 ,
,
+ biến đổi Fourier trong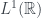 chính là biến đổi Gelfand của đại số
chính là biến đổi Gelfand của đại số 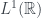 , từ đó dẫn đến
, từ đó dẫn đến
với ,
,
+ chứng minh bất đẳng thức Bernstein cho không gian các hàm nguyên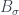 .
.